hlo user manual
| Title | hlo (TXL-based C optimizer) |
| Author | Nikolaos Kavvadias |
| Contact | |
| Website | http://www.nkavvadias.com |
| Release Date | 06 May 2013 |
| Version | 1.5.0 |
| Rev. history | |
| v1.0.0 | 01-12-2011 First official release. |
| v1.1.0 | 09-01-2012 Fixes in partial and full loop unrolling, additions to canonicalization pass, added 16 PolyBench benchmarks. |
| v1.2.0 | 29-02-2012 Added cavity detection (cavdet) benchmark, XML change file generator. |
| v1.3.0 | 15-05-2012 Added files for fixing XML change files. |
| v1.4.0 | 10-06-2012 Converted documentation to RestructuredText; added tutorials and additional information. |
| v1.4.1 | 22-12-2012 Fixed bugs/issues reported: executable naming convention invalid simplification of certain expressions by Ccanon). |
| v1.4.2 | 01-01-2013 New arithmetic-oriented optimizations and documentation update. Removed XML change file generator. |
| v1.5.0 | 06-05-2013 Many updates to arithmetic optimizations. Significant documentation updates. Reworked organization of the current code base. |
1. Introduction
"hlo" is a collection of C-to-C code transformation tools written in the Turing eXtender Language (TXL) (http://www.txl.ca). Each transformation is implemented as a separate executable compiled from the corresponding TXL source file.
"hlo" also includes several auxiliary files such as awk programs, C helper programs and the "kdiv" and "kmul" single constant division and multiplication optimizers.
1.1. Why TXL?
TXL provides the means for developing grammatical transformations without the need to expose internal ASTs. It also allows for agile parsing, which assists in simplifying analyses and optimizations.
2. Obtaining and setting up hlo
Autonomous hlo releases use the hlo-[lin|win]-yymmdd.tar.bz2 naming convention.
- Select lin for Linux or win for Windows binaries release
- yymmdd is the release date
2.1 Obtaining hlo
2.2 Setting up optional tools
For using hlo, a Linux or Windows installation is required. For Windows, Cygwin is suggested (optional) in order to significantly ease the use of hlo.
In any case, standard Unix/Linux tools are expected:
- bash
- make
- diff
- grep
- gawk
For Windows:
- Go to http://sources.redhat.com/cygwin/
- Download the automated web installer (setup.exe)
- Copy it to an empty local directory (e.g. C:\temp\cygwin)
- Click setup.exe
- Select Install from the Internet. Make sure to select make since it might be disabled in the preselection.
Cygwin will then be setup in the C:\cygwin directory of your Windows OS.
For Linux:
- Any recent Linux distribution should do; try using Ubuntu 12.04 LTS.
2.3 hlo setup
There is no actual installation procedure; the user should just unzip the hlo-[lin|win]-yymmdd.tar.bz2 archive to a local directory. Usual choices include C:/cygwin/home/user for Windows/Cygwin users and /home/user for Linux users where user is the name of the current user.
Then, change directory to /home/user/hlo. On Cygwin for instance, type: | $ cd /home/user/hlo
Set up the HLOTOP environmental variable: | $ source env.sh
You may add the /hlo/bin directory to your path: | $ export PATH=$HLOTOP/bin:$PATH
2.4. Building from sources
This subsection is relevant only to the source releases of hlo (hlo-src-yymmdd.tar.bz2). To build hlo from sources the following are required:
- For Linux users:
- A typical Linux installation (bash, make)
- A binary installation of TXL. See http://www.txl.ca (download section) for details. In short, you have to retrieve a TXL release for Linux, uncompress the archive and then run the InstallTxl script:
- Run the build script from the top-level subdirectory:
- For Windows users:
- Windows XP SP2 or Windows 7 (untested on other systems).
- Cygwin environment (bash, make). Cygwin can be installed via an automated web installer (setup.exe) from http://sources.redhat.com/cygwin/
- A binary installation of TXL. See http://www.txl.ca (download section) for details. In short, you have to retrieve a TXL release for Windows (Cygwin release is proposed), uncompress the archive and then run the InstallTxl script:
- Run the build script from the top-level subdirectory of hlo:
3. File listing
The hlo distribution includes the following files. Files denoted by a capital S are not available in binary releases of hlo:
| /hlo | Top-level directory |
S build.sh S clean.sh clean-log.sh clean-suite.sh env.sh hlo.sh run-suite.sh |
Build script for HLO (source only). Cleaning/removal script for HLO (source only). Cleans up the /log subdirectory. Script to clean up debris in the /suite subdirectory. Script to setup the environment (use as: source env.sh) The main script for using HLO transformations. Simple script to exercise the test suite. |
| /hlo/bin | Binaries' directory |
C*.exe c*.sh cygwin1.dll flattenarrinit.exe kdiv.exe kmul.exe |
Executables for applying code transformations (45 files). Run scripts for specific code transformations (12 files). Cygwin DLL for standalone operation on Windows. Lexer for flattening initialization of C arrays. The core executable of the constant division optimizer. The core executable of the constant multiplication optimizer. |
| specialpows.exe | Helper executable for generating TXL rule namings for division and modulo optimizations for specific constants related to powers-of-2. |
| transform.sh | Common script for a number of C-to-C transformations. |
| /hlo/doc | Documentation |
| hlo-flow.dot | Graphviz/DOT file representing a simple proposed flow for using HLO transformations. |
| hlo-flow.png | PNG image showing a graphical view of using HLO transformations. |
MANIFEST README README.GnuC README.html README.pdf |
Complete file listing of the source distribution. This file. README for the TXL GnuC grammar (verbatim copy). HTML version of README. PDF version of README. |
| /hlo/log | Empty directory by default; it is populated by the generated files from running test scripts from /scripts. |
| /hlo/scripts | Scripts' directory |
| run-c*.sh | Test scripts that exercise specific code transformations using small test cases from the /tests subdirectory (25 files). |
| /hlo/src | Source directory with subdirectories for ANSI C, lex, yacc, awk, kdiv, kmul and TXL |
| S /hlo/src/ansic | Directory for ANSI C, lex and yacc sources |
| flattenarrinit.l | Lexer for flattening optimizations of multidimensional arrays in C. |
flattenarrinit.mk specialpows.c |
Makefile for building the flattenarrinit lexer. Generator of TXL rule names and invocations for specific cases of division and modulo optimization. |
| specialpows.mk | Makefile for building the flattenarrinit lexer. |
| /hlo/src/awk | Directory for awk sources |
remblanklines.awk remdupllines.awk |
Removes blank (empty) lines. Removes duplicate lines. |
| /hlo/src/kdiv | Directory for kdiv sources |
| * | Consult /hlo/src/kdiv/README for more details. |
| /hlo/src/kmul | Directory for kmul sources |
| * | Consult /hlo/src/kmul/README for more details. |
| /hlo/src/txl | Directory for TXL sources |
C.Grm C_attrs.Grm |
The TXL GnuC grammar (minor changes against txl.ca). GnuC grammar extensions for expression, declaration and statement attributes. |
NonGNUC.Grm S C*.Txl macros.h |
Pure ANSI C TXL grammar that is not used. TXL source code for each code transformation (45 files). C header file with some common macros. |
| /hlo/suite | Test suite directory |
| *.c | The hlo test suite. Includes 12 applications (divider, eda, edgedet, fir, fsme, mandel, matmult, mc, rcdct, sierpinski, sumarray, tssme). Additionally, some PolyBench applications have been included: 2mm, 3mm, atax, bicg, doitgen, dynprog, gemm, gesummv, mvt, symm, syrk, trmm. |
| /hlo/tests | Regression tests directory |
| *.c | Small test cases for use with the scripts in the /scripts subdirectory. |
4. Supported transformations
Currently, three kinds of transformations are supported: generic restructuring transformations, loop-specific and arithmetic-oriented optimizations.
4.1 Generic restructuring transformations
The first category (generic restructuring transformations - GRT) comprise of the following:
4.2 Loop-specific optimizations
The second category (loop-specific optimizations - LSO) comprise of the following:
4.3 Arithmetic-specific optimizations
The third category (arithmetic-specific optimizations - ASO) comprise of the following:
5. Optimization flow
Fig. hlo-flow illustrates a possible optimization flow using TXL passes. Certain decisions in this flow regard the ordering of transformations, since e.g. loop coalescing prerequisites loop normalization. It should be noted that strip mining eliminates chances for loop unrolling, and should not be applied unconditionally to static loops. Further, it is not meaningful to both use partial and full loop unrolling. User decisions also involve the proper selection of tile size, vector size and unroll factor values by editing hlo.sh. Since many of these transformations produce unoptimized expressions, a code canonicalization pass is re-applied following most transformations.
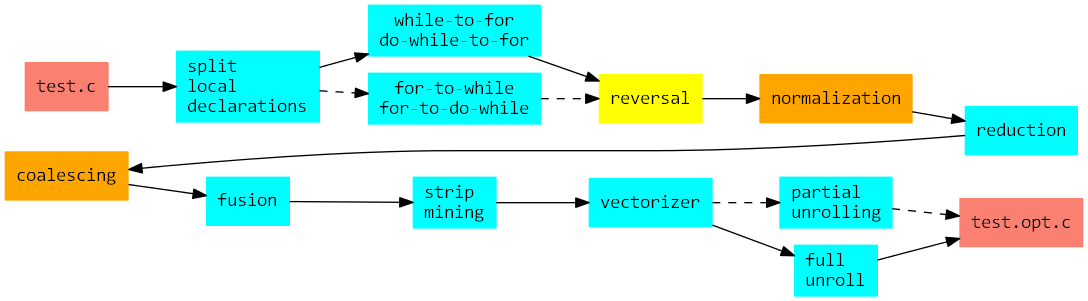
A possible loop-level optimization flow.
6. hlo usage
6.1 Using hlo.sh
hlo is typically used via the hlo.sh bash script.
This script invokes a series of generally applicable code transformations. For example, in order to transform user file myloops.c to myloops.opt.c, the user should do the following:
When invoked properly, the hlo.sh will produce minimal diagnostic printout such as:
:: Canonicalization Split local declarations While-to-for conversion Do-while-to-for conversion Loop normalization Loop reduction Loop coalescing Statement vectorization
The user should define three basic parameters in the hlo.sh script:
- TILESIZE: size for the basic tile regarding strip mining (default: 8).
- UNROLLFACTOR: unroll factor for loop unrolling (default: 8).
- VECTSIZE: size of the vectored statements (default: 8).
The user is responsible for setting these parameters to meaningful values.
6.2 Without using hlo.sh
Access to a single code transformation can be performed into two ways: either through the corresponding /hlo/bin/*.sh script or by directly accessing the transformation executable.
- Example using the dedicated run scripts (assuming testing the /suite files).
- Example directly using the C*.exe executables.
Also, you can use the "-help" switch to get context-specific help for each transformation:
Certain executables have additional options. Code transformations without any runtime parameter, require only specifying the input and output source files, and can be accessed through the transform.sh script.
For instance, to apply for-to-while transformations, the transform.sh script should be used as follows:
As a coding guideline proper bracing of for statements is suggested. for statements that donnot use proper bracing may not be visible to certain transformations.
7. Running the basic tests
The basic tests under the /tests subdirectory can be exercised by running corresponding test scripts:
Results are produced in the /log subdirectory and the following can be used:
to see the optimized version of canon1.c.
Use diff or similar tools to obtain the textual changes between source files:
8. Running the test suite
A more comprehensive test suite using PolyBench kernels is found in the /suite subdirectory. These C source files can be exercised by running the top-level run-suite.sh script.
This suite preprocesses, compiles and runs both the unoptimized (*-ref.c) and optimized (*-opt.c) versions of each test suite file. Results of running the benchmarks are logged to *-ref.txt and *-opt.txt, respectively. Any differences are automatically logged to the standard output.
9. Tutorials
9.1 Enable full and disable partial loop unrolling
The user can always switch off specific transformations and rearrange the order of others. To do this, first open hlo.sh with your favorite ASCII text editor (e.g. gedit, geany would do).
Then, e.g. to disable partial loop unrolling, comment the following lines:
To enable a specific transformation, e.g. full loop unrolling, uncomment the corresponding lines:
9.2 Run an optimized gemm.c
We now have a modified hlo.sh script.
Let's run all the necessary steps to transform, compile and execute gemm.c (as gemm-opt.c).
Here it is assumed that the user already has a preprocessed gemm-ref.c in the /hlo/suite dir, which we can compile:
hlo.sh is invoked to optimize the preprocessed source:
The optimized, source, gemm-opt.c is then compiled:
Both ref and opt versions can be executed to produce printouts:
The generated text files can be compared using diff. Since diff does not report any differences, the diagnostic printouts are identical:
The effect of loop coalescing is clearly visible in the following snippet as found in lines 14-28 of gemm-opt.c.
int i_coalesced1;
for (i_coalesced1 = 0; i_coalesced1 < 65536;
i_coalesced1 = i_coalesced1 + 1) {
i = i_coalesced1 / 256, j = i_coalesced1 % 256;
A[i][j] = ((int) i * j) / 256;
}
int i_coalesced2;
for (i_coalesced2 = 0; i_coalesced2 < 65536;
i_coalesced2 = i_coalesced2 + 1) {
i = i_coalesced2 / 256, j = i_coalesced2 % 256;
B[i][j] = ((int) i * j + 1) / 256;
}
int i_coalesced3;
for (i_coalesced3 = 0; i_coalesced3 < 65536;
i_coalesced3 = i_coalesced3 + 1) {
i = i_coalesced3 / 256, j = i_coalesced3 % 256;
C[i][j] = ((int) i * j + 2) / 256;
}
The application of full loop unrolling is also visible, e.g. in lines 50-307 of gemm-opt.c.
{
C[i][j] += alpha * A[i][0] * B[0][j];
C[i][j] += alpha * A[i][1] * B[1][j];
C[i][j] += alpha * A[i][2] * B[2][j];
C[i][j] += alpha * A[i][3] * B[3][j];
C[i][j] += alpha * A[i][4] * B[4][j];
C[i][j] += alpha * A[i][5] * B[5][j];
C[i][j] += alpha * A[i][6] * B[6][j];
C[i][j] += alpha * A[i][7] * B[7][j];
.....................................
}
9.3 Changing the unroll factor
The unroll factor (defined as P_UNROLLFACTOR) in the hlo.sh script is meaningful when using partial loop unrolling.
The user can edit hlo.sh to set the unroll factor to 4 by changing the corresponding entry:
The hlo.sh script is then edited again in order to disable full loop unrolling and to enable partial loop unrolling.
# Full loop unrolling
# NOTE1: Either use full loop unrolling or partial loop unrolling
echo "Full loop unrolling"
${HLOTOP}/bin/transform.sh loopfullunrolling temp.1 temp.2
cp -f temp.2 temp.1
# Partial loop unrolling
#echo "Partial loop unrolling"
#${HLOTOP}/bin/clooppartialunrolling.sh ${P_UNROLLFACTOR} temp.1 temp.2
#cp -f temp.2 temp.1
${HLOTOP}/bin/transform.sh canon temp.1 temp.2
cp -f temp.2 temp.1
The effect of partial loop unrolling with an unroll factor of 4 is visible in the following optimized main(argc,argv) function:
int main (int argc, char **argv) {
int i, j, k;
init_array ();
int i_coalesced4;
for (i_coalesced4 = 0; i_coalesced4 < 65536;
i_coalesced4 = i_coalesced4 + 1) {
i = i_coalesced4 / 256, j = i_coalesced4 % 256;
C[i][j] *= beta;
for (k = 0; k < 256 - (3);) {
C[i][j] += alpha * A[i][k] * B[k][j];
k = k + 1;
C[i][j] += alpha * A[i][k] * B[k][j];
k = k + 1;
C[i][j] += alpha * A[i][k] * B[k][j];
k = k + 1;
C[i][j] += alpha * A[i][k] * B[k][j];
k = k + 1;
}
for (; k < 256; k = k + 1) {
C[i][j] += alpha * A[i][k] * B[k][j];
}
}
print_array ();
return 0;
}
9.4 Use array flattening
The 3D-to-1D and 2D-to-1D array flattening optimizations are implemented by Carrayflatten.Txl (TXL source for flattening array expressions) and flattenarrinit.l (lexer for flattening initializations).
A simple test case for exercising this transformation can be found in /tests, namely matrix1.c. To produce transformed code for this test, the corresponding script from /scripts can be used:
The optimized file is located in /hlo/log and is named matrix1-out.c.
For instance, array declarations and initializations in matrix1.c:
int karr[2][3]={{1,2,3},{4,5,6}};
int iarr[2][3];
double darr[II][JJ][KK];
char carr[II][2] = {{'A', 'L'},{'M', 'A'}};
float farr[3][5] = {{ 1.1, 1.2, 1.3, -1.4, -1.5},
{ 2.1, 2.2, -2.3, 2.4, 2.5},
{-3.1, -3.2, -3.3, 3.4, 3.5}};
int earr[2][2][2] = {{{1,2},{3,4}},{{5,6},{7,8}}};
are converted to:
int karr [2*3]={1,2,3,4,5,6};
int iarr [2*3];
double darr [II *JJ *KK ];
char carr [II *2]={'A','L','M','A'};
float farr [3*5]={1.1,1.2,1.3,-1.4,-1.5,
2.1,2.2,-2.3,2.4,2.5,-3.1,-3.2,-3.3,3.4,3.5};
int earr [2*2*2]={1,2,3,4,5,6,7,8};
The following two loop nests expose various expressions using 2D and 3D arrays:
for (i = 0; i < 2; i++) {
for (j = 0; j < 3; j++) {
iarr[i][j] = add(karr[i][j], j);
}
}
for (i = 0; i < II; i++) {
for (j = 0; j < JJ; j++) {
for (k = 0; k < KK; k++) {
darr[i][j][k] = (i + j + j + 2.0) / 3.0;
}
}
}
The corresponding transformed nests are as follows:
for (i=0; i<2; i++){
for (j=0; j<3; j++){
iarr [i*3+j] = add (karr [i*3+j], j);
}
}
for (i=0; i<II ; i++){
for (j=0; j<JJ ; j++){
for (k=0; k<KK ; k++){
darr [i*JJ*KK + j*KK + k]=(i+j+j+2.0)/3.0;
}
}
}
9.5 Apply algebraic identities for modulo optimization
Transformation passes Calgdivmod and Calgdivmodspecial deal with optimizing expressions involving modulo computations.
Calgdivmod applies a number of algebraic simplifications, e.g. for replacing constants moduli with smaller ones.
The test case algdivmod1.c exercises all currently implemented identities. To produce transformed code for these tests, the corresponding scripts from /scripts can be used:
As an example, the following expressions:
a = ((f1) * x + (f2)) % x; b = ((f1) * x + (f2)) / x; a = (2*(f1) + 3*(f2)) % 5; b = (2*(f1) + 3*(f2)) / 5; a = (2*(f1)*x + (f2)) % (5*x); b = (2*(f1)*x + (f2)) / (5*x);
are converted to:
a=((f2)%x); b=((f1)+(f2)/x); a=((2%5)*(f1)+(3%5)*(f2))%5; b=((2%5)*(f1)+(3%5)*(f2))/5+(2/5)*(f1)+(3/5)*(f2); a=((2%5)*(f1)*x+(f2))%(5%x); b=((2%5)*(f1)*x+(f2))/(5*x)+(2/5)*(f1);
Transformation Calgdivmodspecial produces optimized code for specific cases of division and modulo by constant, specifically for powers-of-2. In this case, the following assignments:
a = (f1+1) / 4 + 1; b = (f2+2) % 4 + 0; a = (f1) / 16777216 + 1; b = (f2) % 16777216 + 0; aa = (unsigned long long int)(f1+1) / 9223372036854775808 + 1; bb = (unsigned long long int)(f2+2) % 9223372036854775808 + 0;
are converted to:
a=SHL(f1+1,2)+1; b=AND(f2+2,3)+0; a=SHL(f1,24)+1; b=AND(f2,16777215)+0; aa=(unsigned long long int)(f1+1)/9223372036854775808+1; bb=(unsigned long long int)(f2+2)%9223372036854775808+0;
The resulting code uses macro-expansions for computing the logical AND and logical left shift (SHL). These macros are defined in /hlo/src/txl/macros.h.
9.6 Low-level superoptimizations
Superoptimization basically involves the generation of optimal code sequences (usually loop-free) based on exhaustive search of the solution space. While superoptimization itself presents super-exponential time complexity, optimized sequences for short frequently-used straight line code segments are known.
Clowlevelopt replaces occurences of arithmetic expressions and/or function calls for frequently-used computations such as absolute value, minimum and maximum by corresponding superoptimized sequences.
To produce transformed code for the included test cases, use the following:
The test cases lowlevelopt1.c and lowlevelopt2.c exercise various expressions involving abs, min and max. In their initial, pre-optimized form, a sample set of assignments is as follows:
int a, a1, a2; int b, b1, b2; int c, c1, c2; int d, d1, d2; long long int aa, aa1, aa2; long long int bb, bb1, bb2; long long int dd, dd1, dd2; ... c = abs(a); d = min(a, b); dd2 = max(aa2, bb2);
are converted to:
signed int a, b; signed int c, c_t2, c_t3; signed int a1, b1; signed int c1, c1_t2, c1_t3, c1_t4; signed long long int aa2, bb2; signed long long int cc2, cc2_t2, cc2_t3, cc2_t4; c_t2=(a)>>31; c_t3=(a)^c_t2; c=c_t3-c_t2; c1_t2=a1^b1; c1_t3=-((u32)a1<=(u32)b1); c1_t4=c1_t2&c1_t3; c1=c1_t4^b1; cc2_t2=aa2^bb2; cc2_t3=-((u64)aa2>=(u64)bb2); cc2_t4=cc2_t2&cc2_t3; cc2=cc2_t4^bb2;
In this version, additive, subtractive, multiplicative and other complex expressions as function arguments are not supported for optimization.
9.7 Constant multiplication optimization
Ckmulopt replaces multiplications by constant by calls to corresponding multiplierless routines and incorporates the routines themselves into the resulting transformed code.
To produce transformed code for the included test case named kmuldiv1.c, the corresponding script can be used:
As of current, three-address code like assignments can be transformed, as can be seen below. First, the initial code segment is shown:
int func1(int);
int func2(void);
int main(int argc, char *argv[]) {
int a, b, c, d, e;
a = atoi(argv[1]);
b = a * 3;
c = b / 11;
d = func1(c) * 17;
e = d + func2() / 7;
return (c+d+e);}
The resulting code is as follows:
int func1(int);
int func2(void);
int main(int argc,char*argv[]){
signed int a, b, c, d, e;
a=atoi (argv[1]);
b=kmul_s32_p_3 (a);
c=b/11;
d=func1 (c)*17;
e=d+func2 ()/7;
return(c+d+e);}
signed int kmul_s32_p_3(signed int x){
signed int t0, t1, t2;
signed int y;
t0=x;
t1=t0<<1;
t2=t1+x;
y=t2;
return(y);}
9.8 Constant division optimization
Ckdivopt replaces divisions by constant by calls to corresponding divisionless routines and incorporates the routines themselves into the resulting transformed code.
To produce transformed code for the included test case named kmuldiv1.c, the corresponding script can be used from within /hlo/scripts:
As of current, three-address code like assignments can be transformed, as can be seen below.
For the same initial code segment as in the case of constant multiplication optimization, the following code is produced:
int func1(int);
int func2(void);
int main(int argc,char*argv[]){
signed int a, b, c, d, e;
a=atoi (argv[1]);
b=a*3;
c=kdiv_s32_p_11 (b);
d=func1 (c)*17;
e=d+func2 ()/7;
return(c+d+e);}
signed int kdiv_s32_p_11(signed int n){
signed int q,M=780903145,c;
signed long long int t,u,v;
t=(signed long long int)M*(signed long long int)n;
q=t>>32;
q=q>>1;
c=n>>31;
q=q+c;
return(q);}
9.9 Optimization by Horner scheme
Syntactic transformations of polynomial expressions to optimized forms are still work in progress. However, Chornerpolyopt applies such transformations to explicit polynomials, up to the 8th degree. This covers must usual cases of polynomial expressions, as in computer graphics (where quartic and quintic polynomials are often used).
To produce transformed code for the included test case named polyopt1.c, the corresponding script can be used from within /hlo/scripts:
First, the initial code segment is shown:
f1 = 1 + x; f2 = 1 + 2*x + x*x; f3 = 1 + 2*x + x*x + 3*x*x*x; f4 = 5 + 2*x + x*x + 3*x*x*x - 4*x*x*x*x; f5 = 0 + 2*x + x*x - 11*x*x*x + x*x*x*x - x*x*x*x*x; ...
The resulting code is as follows:
f1=1+x; f2=1+x*(2+x); f3=1+x*(2+x*(1+x*(3))); f4=5+x*(2+x*(1+x*(3-x*(4)))); f5=0+x*(2+x*(1-x*(11+x*(1-x))));
10. Known problems and issues
There are certain known problems regarding this release of hlo. For most cases, a solution will be developed in the immediate future.
Known issues:
- Loop fusion requires that the user checks that data dependencies are respected.
- Loop unswitching is currently being fixed.
- Certain transformations generate variables in local C scope. This is acceptable C99 practice, but is not supported by some C89 compilers, such as the HP VEX compiler. This means that e.g. strip mining should be avoid for VEX compilation.
- Comments are not maintained through transformation passes.
- Loop unrolling (partial, full) works on single statement loop bodies.
- hlo follows the C.Grm GNU C grammar with minor changes. In case of user code that appears non-compliant, please check first against the plain TXL-based parser, e.g.:
- It is suggested that proper bracing is used for while, for and do-while statements.
- Macros from macros.h are not yet automatically incorporated in resulting files.
- Clowlevelopt.Txl needs to be expanded for taking account further superoptimized code sequences.
- Clowlevelopt.Txl does not yet optimize functions with complex expressions as function arguments.
- Ckmulopt and Ckdivopt expect operations by constant in a three-address code like form.
11. Contact
You may contact me for further questions/suggestions/corrections at: